Columns - Analysis

RISAFloor performs an analysis of columns by taking the individual floor results and using a Modified Hardy-Cross method to distribute moments through the column stack. Here we will talk about some of the details of the RISAFloor column analysis.

Note:

• For modeling and general information on columns see the Columns - Modeling topic.
• For column results information see the Columns - Results topic.

Multi-Story Column Analysis

RISAFloor designs a structure in a top to bottom manner, thus following load path. At each floor in the model the loads are brought down and applied to the floor below. This can creates some challenges for column analysis in multi-story applications in certain situations. It may be considered as follows:

1. The uppermost floor is analyzed and beams and columns are designed. We will see below that the column size affects the moment distribution to the beams.
2. We then go to the next floor down and the column size taken from the floor above is used in the analysis of the next floor down. During this analysis the beams and columns are again designed.  It is probable that the column will need to be upsized due to the additional forces it is seeing from this floor. This upsizing will be considered properly on this floor and the floors below.  However, the top-most floor has already been designed/analyzed. The program does not automatically iterate the column for all floors and keep running solutions. This could cause iterative loops that do not converge on a solution.
3. Instead, after solution the program gives the dialog box below. This gives a list of all columns which analysis and design sections were different. We then give an option to continue or re-solve.

   1. 

4. If the "Analysis Shape" and "Final Shape" are very close in size then this difference is likely small. In this case you may choose the OK option which will finish the solution and give results with the mismatched analysis/design sizes. If these shapes are very different then you may choose RESOLVE and an entirely new solution will be run with the analysis shape updated accordingly.  Note that you may need to resolve several times if this situation occurs again with the new solution.

Lateral Support From Floor/Slab Levels and Framing Elements

Columns that are multi-story that pass through multiple floors will be checked to determine whether an individual floor provides lateral support. A floor will provide lateral support for a column (for both analysis and design) if:

1. The column passes through a deck or slab.
2. The column has a beam or beams that frame into it that are not outrigger beams. There are some small differences between analysis and design that will be explained.

If a beam frames into the column it will brace the column in the direction it is framing in. If a beam frames in that is not in the direction of column local axes then there is different behavior for analysis and design.

Lateral Support for Design (Unbraced Length) Considerations.

For design considerations the beam will brace the direction it would physically frame into. For example, if a beam frames into a wide flange member the program will check to see if the centerline of the beam hits the flange or the web.  If it hits the web it will brace the local y-y direction.  If it hits the flange it will brace the z-z direction. A beam that frames in at 45 degrees will brace both column local axes. The example below will brace the y-y direction.

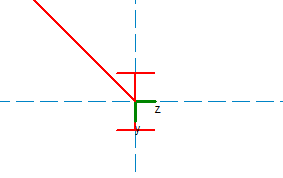
The exception to this occurs if a member frames right at the interface between the strong and weak direction. In that case the program assumes the member is braced only in the z-z direction. See the example below where a concrete beam frames into a square concrete column at a 45 degree angle.  In this situation the column is only braced about it's strong axis (z-z) and is not considered braced at this level about it's weak axis (y-y).

Lateral Support for Analysis Considerations.

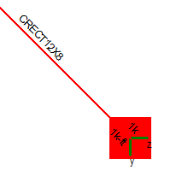
For analysis, if a beam frames in directly along the local axes of the column then the column is only braced in that local axis direction. If a skewed beam frames into a column then it is assumed that the beam braces BOTH local directions, regardless of the angle of the member framing in. In the example below the beam physically frames into the left face of column.  However, because it is a skewed member it will be considered to brace the column in both directions for analysis.

Column Moments and Shears - Eccentricity

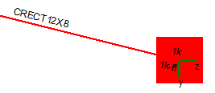
For columns with members framing in without eccentricity the column will be an axial-force only element and the analysis is trivial. However, there are several different ways in which moments can be introduced to columns in RISAFloor. Aside from carrying a moment from higher or lower in the column stack, a column can pick up a moment at a floor from the following methods:

• Beams which have fixed-ends and which frame directly into the column.
• Beams which have pinned-ends and which have Column Eccentricity turned on in their Connection Properties
• Slab moments that will be transferred into the column (RISAFloor ES only)

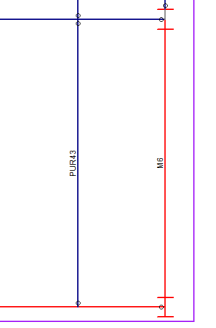
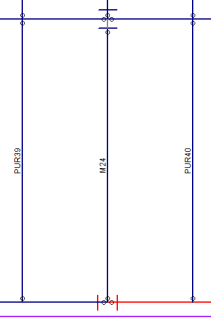
Fixed-End Beams M6 has fixed end releases on either end, which will impart moment forces into the columns accordingly.	Pinned-End Beams M24 has Column Eccentricity turned on. Thus, there is an eccentricity defined that will impart a moment to the columns based on the reaction * eccentricity.	Slab Floor (Floor ES only) The slab will be moment connected to the column automatically

Fixed-End Beams and Slab Floors

Fixed-end beams can only transfer moment into a column when the Use Column Stiffness checkbox has been checked on the Model Settings.

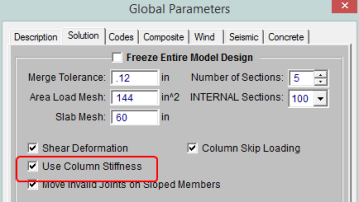
When this is enabled the column's rotational stiffness is approximated for each axis and is considered in the stiffness matrix solution for that floor. Because RISAFloor performs an independent stiffness matrix solution for each floor the column's rotational stiffness is represented (behind the scenes) as a rotational spring boundary condition. This results in some moment redistribution and can therefore affect the amount of moment which the beam carries.

The amount of rotational stiffness provided by the column (rotational spring boundary condition) is influenced by the following factors:

• The rotational stiffness (E*I) of the column
• The distance (L) from the floor level in question to the floors immediately above and below
• The rotational stiffness of the fixed-end beams on the floors immediately above and below the floor level in question

The resultant joint reaction (moment) from the stiffness matrix solution at the spring boundary condition is then distributed to the column. The amount of moment which is sent to the portion of the column above the floor (versus the portion below the floor) is determined using a simplified version of the Hardy Cross Moment Distribution Method.

Note: 

• Column flexural properties (E, I and floor heights) are used to determine the distribution factors in the Hardy Cross Moment Distribution Method in the same way they are used to approximate the column rotational stiffnesses.
• The applied moments at each floor are taken directly from the independent stiffness matrix solution for that floor.
• This method is intended to function as a good approximation of the true moments. However, this method does not take into account shear deformation or the presence of axial loads or deformations.
• The Hardy Cross moments only affect the column moments, not any beams that are fixed to the columns. This can result in unbalanced moment between the beam and column.
• The final design of column and beams which require the consideration of three dimensional effects (i.e. moment frames or columns that are supported by transfer girders) should always be performed in RISA-3D. This is because RISA-3D will use a full three dimensional stiffness matrix solution to solve for all forces and moments.

Pinned-End Beams

Pinned-end beams can only transfer moment into a column when the Column Eccentricity flag has been checked in the Connections tab of the Beams spreadsheet.

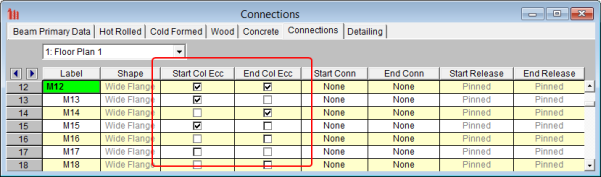
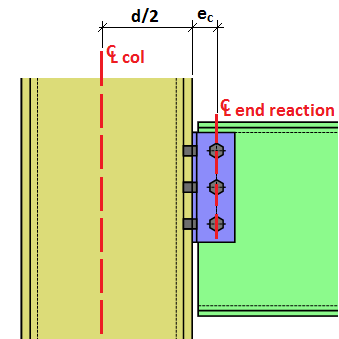
The moment introduced into the column is calculated using the following formula:

M_column = R_beam*((d_column/2) + e_connection)

where

R = Beam end reaction

d = Column depth in the direction which the beam frames into the column (d for strong axis, b for weak axis)

e = Eccentricity between the face of the column and the beam's end reaction resultant

Note:

• Only Hot Rolled Steel beams may be assigned an eccentricity.
• Beams which are skewed (not parallel to either of the column's local axes) will receive a geometrically increased offset to account for the additional eccentricity caused by the additional depth of column.
• For beams framing into the web of Wide Flange columns the value (d/2) is taken as zero.
• The moment caused by eccentricity is ignored for beams framing into the top of columns that have a Pinned top fixity.

Column Skip Loading

This feature is only enabled when it has been activated in the Model Settings.

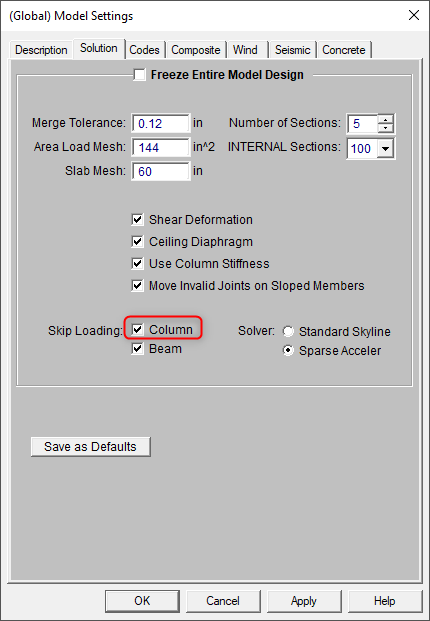
When enabled the program automatically checks for the worst-case unbalanced loading on the columns. The methodology is explained below:

• The program determines the shear and moment end reactions (including moment caused by eccentricity) for each beam that frames into a given column.
• All beams which frame into that column are lumped into four "quadrants", each representing a cardinal direction relative to the column.
  • These quadrants are illustrated in the Detail Report as LL1, LL2, LL3, and LL4. They are relative to the column's local axes.
  • Skewed beams are assigned to the nearest quadrant. Their end reaction is assumed to act entirely within that quadrant.

• During solution the dead load (DL) including Self Weight, PreDL, PostDL, and Const DL is assumed to be fully applied for all four quadrants for all permutations.
• During solution the program solves each permutation of live load patterns for each load combination at each floor of a column lift. While checking the various patterns at a given floor all other floors are assumed to be fully-loaded
• The code check value reported for the column is based on the controlling load combination, with the controlling pattern applied on the controlling floor, and all other floors for that column taken as fully loaded (i.e. the pattern at all other floors is DL + LL1 + LL2 + LL3 + LL4).
• Separate patterns are determined for the Bending/Axial code check and the Shear code check.
• Columns with cantilevers are not skip loaded in the direction of the cantilever. This is unnecessary because the analysis results properly apportion the cantilever moments based on relative rigidity of the back span beam and supporting column.

• Skip loaded LL moments are carried up and down the column stack by quadrant. The worst case unbalanced load in each quadrant for each floor level is used for hardy cross moment redistribution and for the design.

Note:

• A wide flange image is used in the detail report regardless of the actual shape type assigned to the column. This is for strong/weak axis clarity.

Hanger Columns

Hanger columns can be drawn to support a mezzanine floor. A mezzanine floor is like a typical floor with the only difference being that the floor is supported by hanger columns from the floor above. Therefore, the loads originating from the mezzanine floor will distribute to the hanger columns and then ultimately to the floor above. The hanger column must start from a supporting beam from the floor above and can only support the floor directly beneath. Steps to draw hanger column is presented in To Draw Hanger Columns.

Limitations:

• Hanger columns can only support a single floor at this time.
• Hanger columns can only be Hot Rolled, Cold Formed, or Wood shapes.
• Hanger columns can only be drawn for Beam Supported Floors.
• Hanger columns cannot be supported by walls or columns below.
• Hanger columns cannot be drawn from framing members that are supported by hanger columns.
• No outriggers are allowed on hanger columns.